Уравнение прямой в отрезках: описание, примеры, решение задач. Прямая линия. Уравнение прямой Уравнение прямой, проходящей через данную точку

Свойства прямой в евклидовой геометрии.

Через любую точку можно провести бесконечно много прямых.

Через любые две несовпадающие точки можно провести единственную прямую.

Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются

параллельными (следует из предыдущего).

В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:

• прямые пересекаются;

• прямые параллельны;

• прямые скрещиваются.

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия

задается на плоскости уравнением первой степени (линейное уравнение).

Общее уравнение прямой.

Определение . Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим

уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

. C = 0, А ≠0, В ≠ 0 - прямая проходит через начало координат

. А = 0, В ≠0, С ≠0 { By + C = 0} - прямая параллельна оси Ох

. В = 0, А ≠0, С ≠ 0 { Ax + C = 0} - прямая параллельна оси Оу

. В = С = 0, А ≠0 - прямая совпадает с осью Оу

. А = С = 0, В ≠0 - прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких - либо заданных

начальных условий.

Уравнение прямой по точке и вектору нормали.

Определение . В декартовой прямоугольной системе координат вектор с компонентами (А, В)

перпендикулярен прямой, заданной уравнением

Ах + Ву + С = 0.

Пример . Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение . Составим при А = 3 и В = -1 уравнение прямой: 3х - у + С = 0. Для нахождения коэффициента С

подставим в полученное выражение координаты заданной точки А. Получаем: 3 - 2 + C = 0, следовательно

С = -1. Итого: искомое уравнение: 3х - у - 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть в пространстве заданы две точки M 1 (x 1 , y 1 , z 1) и M2 (x 2, y 2 , z 2), тогда уравнение прямой ,

проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На

плоскости записанное выше уравнение прямой упрощается:

если х 1 ≠ х 2 и х = х 1 , если х 1 = х 2 .

Дробь = k называется угловым коэффициентом прямой .

Пример . Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение . Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется

уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание

прямой через точку и направляющий вектор прямой.

Определение . Каждый ненулевой вектор (α 1 , α 2) , компоненты которого удовлетворяют условию

Аα 1 + Вα 2 = 0 называется направляющим вектором прямой.

Ах + Ву + С = 0.

Пример . Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение . Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,

коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

при х = 1, у = 2 получаем С/ A = -3 , т.е. искомое уравнение:

х + у - 3 = 0

Уравнение прямой в отрезках.

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на -С, получим:

или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения

прямой с осью Ох, а b - координатой точки пересечения прямой с осью Оу.

Пример . Задано общее уравнение прямой х - у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется

нормирующем множителем , то получим

xcosφ + ysinφ - p = 0 - нормальное уравнение прямой .

Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0.

р - длина перпендикуляра, опущенного из начала координат на прямую,

а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Пример . Дано общее уравнение прямой 12х - 5у - 65 = 0 . Требуется написать различные типы уравнений

этой прямой.

Уравнение этой прямой в отрезках :

Уравнение этой прямой с угловым коэффициентом : (делим на 5)

Уравнение прямой :

cos φ = 12/13; sin φ= -5/13; p = 5.

Следует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые,

параллельные осям или проходящие через начало координат.

Угол между прямыми на плоскости.

Определение . Если заданы две прямые y = k 1 x + b 1 , y = k 2 x + b 2 , то острый угол между этими прямыми

будет определяться как

Две прямые параллельны, если k 1 = k 2 . Две прямые перпендикулярны,

если k 1 = -1/ k 2 .

Теорема .

Прямые Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 параллельны, когда пропорциональны коэффициенты

А 1 = λА, В 1 = λВ . Если еще и С 1 = λС , то прямые совпадают. Координаты точки пересечения двух прямых

находятся как решение системы уравнений этих прямых.

Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой.

Определение . Прямая, проходящая через точку М 1 (х 1 , у 1) и перпендикулярная к прямой у = kx + b

представляется уравнением:

Расстояние от точки до прямой.

Теорема . Если задана точка М(х 0 , у 0), то расстояние до прямой Ах + Ву + С = 0 определяется как:

Доказательство . Пусть точка М 1 (х 1 , у 1) - основание перпендикуляра, опущенного из точки М на заданную

прямую. Тогда расстояние между точками М и М 1 :

(1)

Координаты x 1 и у 1 могут быть найдены как решение системы уравнений:

Второе уравнение системы - это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно

заданной прямой. Если преобразовать первое уравнение системы к виду:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.

Уравнение прямой на плоскости.
Направляющий вектор прямой. Вектор нормали

Прямая линия на плоскости – это одна из простейших геометрических фигур, знакомая вам ещё с младших классов, и сегодня мы узнаем, как с ней справляться методами аналитической геометрии. Для освоения материала необходимо уметь строить прямую; знать, каким уравнением задаётся прямая, в частности, прямая, проходящая через начало координат и прямые, параллельные координатным осям. Данную информацию можно найти в методичке Графики и свойства элементарных функций , я её создавал для матана, но раздел про линейную функцию получился очень удачным и подробным. Поэтому, уважаемые чайники, сначала разогрейтесь там. Кроме того, нужно обладать базовыми знаниями о векторах , иначе понимание материала будет неполным.

На данном уроке мы рассмотрим способы, с помощью которых можно составить уравнение прямой на плоскости. Рекомендую не пренебрегать практическими примерами (даже если кажется очень просто), так как я буду снабжать их элементарными и важными фактами, техническими приёмами, которые потребуются в дальнейшем, в том числе и в других разделах высшей математики.

• Как составить уравнение прямой с угловым коэффициентом?
• Как ?
• Как найти направляющий вектор по общему уравнению прямой?
• Как составить уравнение прямой по точке и вектору нормали?

и мы начинаем:

Уравнение прямой с угловым коэффициентом

Всем известный «школьный» вид уравнения прямой называется уравнением прямой с угловым коэффициентом . Например, если прямая задана уравнением , то её угловой коэффициент: . Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:

В курсе геометрии доказывается, что угловой коэффициент прямой равен тангенсу угла между положительным направлением оси и данной прямой : , причём угол «откручивается» против часовой стрелки.

Чтобы не загромождать чертёж, я нарисовал углы только для двух прямых. Рассмотрим «красную» прямую и её угловой коэффициент . Согласно вышесказанному: (угол «альфа» обозначен зелёной дугой). Для «синей» прямой с угловым коэффициентом справедливо равенство (угол «бета» обозначен коричневой дугой). А если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Как говорится, тригонометрическая таблица или микрокалькулятор в руки. Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс .

При этом возможны следующие случаи:

1) Если угловой коэффициент отрицателен: , то линия, грубо говоря, идёт сверху вниз. Примеры – «синяя» и «малиновая» прямые на чертеже.

2) Если угловой коэффициент положителен: , то линия идёт снизу вверх. Примеры – «чёрная» и «красная» прямые на чертеже.

3) Если угловой коэффициент равен нулю: , то уравнение принимает вид , и соответствующая прямая параллельна оси . Пример – «жёлтая» прямая.

4) Для семейства прямых , параллельных оси (на чертеже нет примера, кроме самой оси ), углового коэффициента не существует (тангенс 90 градусов не определён) .

Чем больше угловой коэффициент по модулю, тем круче идёт график прямой .

Например, рассмотрим две прямые . Здесь , поэтому прямая имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.

В свою очередь, прямая более крутА, чем прямые .

Обратно: чем меньше угловой коэффициент по модулю, тем прямая является более пологой .

Для прямых справедливо неравенство , таким образом, прямая более полога. Детская горка, чтобы не насадить себе синяков и шишек.

Зачем это нужно?

Продлить ваши мучения Знания вышеперечисленных фактов позволяет немедленно увидеть свои ошибки, в частности, ошибки при построении графиков – если на чертеже получилось «явно что-то не то». Желательно, чтобы вам сразу было понятно, что, например, прямая весьма крутА и идёт снизу вверх, а прямая – очень полога, близко прижата к оси и идёт сверху вниз.

В геометрических задачах часто фигурируют несколько прямых, поэтому их удобно как-нибудь обозначать.

Обозначения : прямые обозначаются маленькими латинскими буквами: . Популярный вариант – обозначение одной и той же буквой с натуральными подстрочными индексами. Например, те пять прямых, которые мы только что рассмотрели, можно обозначить через .

Поскольку любая прямая однозначно определяется двумя точками, то её можно обозначать данными точками: и т.д. Обозначение совершенно очевидно подразумевает, что точки принадлежат прямой .

Пора немного размяться:

Как составить уравнение прямой с угловым коэффициентом?

Если известна точка , принадлежащая некоторой прямой, и угловой коэффициент этой прямой, то уравнение данной прямой выражается формулой :

Пример 1

Составить уравнение прямой с угловым коэффициентом , если известно, что точка принадлежит данной прямой.

Решение : Уравнение прямой составим по формуле . В данном случае:

Ответ :

Проверка выполняется элементарно. Во-первых, смотрим на полученное уравнение и убеждаемся, что наш угловой коэффициент на своём месте. Во-вторых, координаты точки должны удовлетворять данному уравнению. Подставим их в уравнение:

Получено верное равенство, значит, точка удовлетворяет полученному уравнению.

Вывод : уравнение найдено правильно.

Более хитрый пример для самостоятельного решения:

Пример 2

Составить уравнение прямой, если известно, что её угол наклона к положительному направлению оси составляет , и точка принадлежит данной прямой.

Если возникли затруднения, перечитайте теоретический материал. Точнее больше практический, многие доказательства я пропускаю.

Прозвенел последний звонок, отгремел выпускной бал, и за воротами родной школы нас поджидает, собственно, аналитическая геометрия. Шутки закончились…. А может быть только начинаются =)

Ностальгически машем ручкой привычному и знакомимся с общим уравнением прямой. Поскольку в аналитической геометрии в ходу именно оно:

Общее уравнение прямой имеет вид : , где – некоторые числа. При этом коэффициенты одновременно не равны нулю, так как уравнение теряет смысл.

Оденем в костюм и галстук уравнение с угловым коэффициентом . Сначала перенесём все слагаемые в левую часть:

Слагаемое с «иксом» нужно поставить на первое место:

В принципе, уравнение уже имеет вид , но по правилам математического этикета коэффициент первого слагаемого (в данном случае ) должен быть положительным. Меняем знаки:

Запомните эту техническую особенность! Первый коэффициент (чаще всего ) делаем положительным!

В аналитической геометрии уравнение прямой почти всегда будет задано в общей форме. Ну, а при необходимости его легко привести к «школьному» виду с угловым коэффициентом (за исключением прямых, параллельных оси ординат).

Зададимся вопросом, что достаточно знать, чтобы построить прямую? Две точки. Но об этом детском случае позже, сейчас властвуют палочки со стрелочками. У каждой прямой есть вполне определённый наклон, к которому легко «приспособить» вектор .

Вектор, который параллелен прямой, называется направляющим вектором данной прямой . Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – не важно).

Направляющий вектор я буду обозначать следующим образом: .

Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости. Поэтому дополнительно необходимо знать некоторую точку , которая принадлежит прямой.

Как составить уравнение прямой по точке и направляющему вектору?

Если известна некоторая точка , принадлежащая прямой, и направляющий вектор этой прямой , то уравнение данной прямой можно составить по формуле :

Иногда его называют каноническим уравнением прямой .

Что делать, когда одна из координат равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты не могут равняться нулю, так как нулевой вектор не задаёт конкретного направления.

Пример 3

Составить уравнение прямой по точке и направляющему вектору

Решение : Уравнение прямой составим по формуле . В данном случае:

С помощью свойств пропорции избавляемся от дробей:

И приводим уравнение к общему виду:

Ответ :

Чертежа в таких примерах, как правило, делать не нужно, но понимания ради:

На чертеже мы видим исходную точку , исходный направляющий вектор (его можно отложить от любой точки плоскости) и построенную прямую . Кстати, во многих случаях построение прямой удобнее всего осуществлять как раз с помощью уравнения с угловым коэффициентом. Наше уравнение легко преобразовать к виду и без проблем подобрать ещё одну точку для построения прямой.

Как отмечалось в начале параграфа, у прямой бесконечно много направляющих векторов, и все они коллинеарны. Для примера я нарисовал три таких вектора: . Какой бы направляющий вектор мы не выбрали, в результате всегда получится одно и то же уравнение прямой .

Составим уравнение прямой по точке и направляющему вектору :

Разруливаем пропорцию:

Делим обе части на –2 и получаем знакомое уравнение:

Желающие могут аналогичным образом протестировать векторы или любой другой коллинеарный вектор.

Теперь решим обратную задачу:

Как найти направляющий вектор по общему уравнению прямой?

Очень просто:

Если прямая задана общим уравнением , то вектор является направляющим вектором данной прямой.

Примеры нахождения направляющих векторов прямых:

Утверждение позволяет найти лишь один направляющий вектор из бесчисленного множества, но нам больше и не нужно. Хотя в ряде случаев координаты направляющих векторов целесообразно сократить:

Так, уравнение задаёт прямую, которая параллельна оси и координаты полученного направляющего вектора удобно разделить на –2, получая в точности базисный вектор в качестве направляющего вектора. Логично.

Аналогично, уравнение задаёт прямую, параллельную оси , и, разделив координаты вектора на 5, получаем в качестве направляющего вектора орт .

Теперь выполним проверку Примера 3 . Пример уехал вверх, поэтому напоминаю, что в нём мы составили уравнение прямой по точке и направляющему вектору

Во-первых , по уравнению прямой восстанавливаем её направляющий вектор: – всё нормально, получили исходный вектор (в ряде случаев может получиться коллинеарный исходному вектор, и это обычно несложно заметить по пропорциональности соответствующих координат).

Во-вторых , координаты точки должны удовлетворять уравнению . Подставляем их в уравнение:

Получено верное равенство, чему мы очень рады.

Вывод : задание выполнено правильно.

Пример 4

Составить уравнение прямой по точке и направляющему вектору

Это пример для самостоятельного решения. Решение и ответ в конце урока. Крайне желательно сделать проверку по только что рассмотренному алгоритму. Старайтесь всегда (если это возможно) выполнять проверку на черновике. Глупо допускать ошибки там, где их 100%-но можно избежать.

В том случае, если одна из координат направляющего вектора нулевая, поступают очень просто:

Пример 5

Решение : Формула не годится, так как знаменатель правой части равен нулю. Выход есть! Используя свойства пропорции, перепишем формулу в виде , и дальнейшее покатилось по глубокой колее:

Ответ :

Проверка :

1) Восстановим направляющий вектор прямой :
– полученный вектор коллинеарен исходному направляющему вектору.

2) Подставим координаты точки в уравнение :

Получено верное равенство

Вывод : задание выполнено правильно

Возникает вопрос, зачем маяться с формулой , если существует универсальная версия , которая сработает в любом случае? Причин две. Во-первых, формула в виде дроби гораздо лучше запоминается . А во-вторых, недостаток универсальной формулы состоит в том, что заметно повышается риск запутаться при подстановке координат.

Пример 6

Составить уравнение прямой по точке и направляющему вектору .

Это пример для самостоятельного решения.

Вернёмся к вездесущим двум точкам:

Как составить уравнение прямой по двум точкам?

Если известны две точки , то уравнение прямой, проходящей через данные точки, можно составить по формуле:

На самом деле это разновидность формулы и вот почему: если известны две точки , то вектор будет направляющим вектором данной прямой. На уроке Векторы для чайников мы рассматривали простейшую задачу – как найти координаты вектора по двум точкам. Согласно данной задаче, координаты направляющего вектора:

Примечание : точки можно «поменять ролями» и использовать формулу . Такое решение будет равноценным.

Пример 7

Составить уравнение прямой по двум точкам .

Решение : Используем формулу:

Причёсываем знаменатели:

И перетасовываем колоду:

Именно сейчас удобно избавиться от дробных чисел. В данном случае нужно умножить обе части на 6:

Раскрываем скобки и доводим уравнение до ума:

Ответ :

Проверка очевидна – координаты исходных точек должны удовлетворять полученному уравнению:

1) Подставим координаты точки :

Верное равенство.

2) Подставим координаты точки :

Верное равенство.

Вывод : уравнение прямой составлено правильно.

Если хотя бы одна из точек не удовлетворяет уравнению, ищите ошибку.

Стоит отметить, что графическая проверка в данном случае затруднительна, поскольку построить прямую и посмотреть, принадлежат ли ей точки , не так-то просто.

Отмечу ещё пару технических моментов решения. Возможно, в данной задаче выгоднее воспользоваться зеркальной формулой и, по тем же точкам составить уравнение:

Таки дробей поменьше. Если хотите, можете довести решение до конца, в результате должно получиться то же самое уравнение.

Второй момент состоит в том, чтобы посмотреть на итоговый ответ и прикинуть, нельзя ли его ещё упростить? Например, если получилось уравнение , то здесь целесообразно сократить на двойку: – уравнение будет задавать ту же самую прямую. Впрочем, это уже тема разговора о взаимном расположении прямых .

Получив ответ в Примере 7, я на всякий случай, проверил, не делятся ли ВСЕ коэффициенты уравнения на 2, 3 или 7. Хотя, чаще всего подобные сокращения осуществляются ещё по ходу решения.

Пример 8

Составить уравнение прямой, проходящей через точки .

Это пример для самостоятельного решения, который как раз позволит лучше понять и отработать технику вычислений.

Аналогично предыдущему параграфу: если в формуле один из знаменателей (координата направляющего вектора) обращается в ноль, то переписываем её в виде . И снова заметьте, как неуклюже и запутанно она стала выглядеть. Не вижу особого смысла приводить практические примеры, поскольку такую задачу мы уже фактически прорешали (см. № 5, 6).

Вектор нормали прямой (нормальный вектор)

Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), причём все векторы нормали прямой будут коллинеарными (сонаправленными или нет – без разницы).

Разборки с ними будут даже проще, чем с направляющими векторами:

Если прямая задана общим уравнением в прямоугольной системе координат, то вектор является вектором нормали данной прямой.

Если координаты направляющего вектора приходится аккуратно «вытаскивать» из уравнения, то координаты вектора нормали достаточно просто «снять».

Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения :

Приведу примеры с теми же уравнениями, что и для направляющего вектора:

Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Если известен вектор нормали, то однозначно определено и направление самой прямой – это «жёсткая конструкция» с углом в 90 градусов.

Как составить уравнение прямой по точке и вектору нормали?

Если известна некоторая точка , принадлежащая прямой, и вектор нормали этой прямой, то уравнение данной прямой выражается формулой :

Тут всё обошлось без дробей и прочих нежданчиков. Такой вот у нас нормальный вектор. Любите его. И уважайте =)

Пример 9

Составить уравнение прямой по точке и вектору нормали . Найти направляющий вектор прямой.

Решение : Используем формулу:

Общее уравнение прямой получено, выполним проверку:

1) «Снимаем» координаты вектора нормали с уравнения : – да, действительно, получен исходный вектор из условия (либо должен получиться коллинеарный исходному вектор).

2) Проверим, удовлетворяет ли точка уравнению :

Верное равенство.

После того, как мы убедились в том, что уравнение составлено правильно, выполним вторую, более лёгкую часть задания. Вытаскиваем направляющий вектор прямой:

Ответ :

На чертеже ситуация выглядит следующим образом:

В целях тренировки аналогичная задача для самостоятельного решения:

Пример 10

Составить уравнение прямой по точке и нормальному вектору . Найти направляющий вектор прямой.

Заключительный раздел урока будет посвящен менее распространённым, но тоже важным видам уравнений прямой на плоскости

Уравнение прямой в отрезках.
Уравнение прямой в параметрической форме

Уравнение прямой в отрезках имеет вид , где – ненулевые константы. Некоторые типы уравнений нельзя представить в таком виде, например, прямую пропорциональность (так как свободный член равен нулю и единицу в правой части никак не получить).

Это, образно говоря, «технический» тип уравнения. Обыденная задача состоит в том, чтобы общее уравнение прямой представить в виде уравнения прямой в отрезках . Чем оно удобно? Уравнение прямой в отрезках позволяет быстронайти точки пересечения прямой с координатными осями, что бывает очень важным в некоторых задачах высшей математики.

Найдём точку пересечения прямой с осью . Обнуляем «игрек», и уравнение принимает вид . Нужная точка получается автоматически: .

Аналогично с осью – точка, в которой прямая пересекает ось ординат.

Пусть задана некоторая афинная система координат OXY.

Теорема 2.1. Любая прямая l системе координат ОX задается линейным уравнением вида

Аx + By + С = О, (1)

где А, В, С R и А 2 + В 2 0. Обратно, любое уравнение вида (1) задает прямую.

Уравнение вида (1) - общее уравнение прямой .

Пусть в уравнении (1) все коэффициенты А, В и С отличны от нуля. Тогда

Ах-By=-С, и .

Обозначим -С/А=а, -С/B=b. Получим

-уравнение в отрезках .

Действительно, числа |а| и |b| указывают на величины отрезков, отсекаемых прямой l на осях ОХ и OY соответственно.

Пусть прямая l задана общим уравнением (1) в прямоугольной системе координат и пусть точки M 1 (x 1 ,у 1) и М 2 (х 2 ,у 2) принадлежит l . Тогда

Аx 1 + Ву 1 + С = Ах 2 + Ву 2 + С, то есть A(x 1 -x 2) + В(у 1 -у 2) = 0.

Последнее равенство означает, что вектор =(А,В) ортогонален вектору =(x 1 -x 2 ,у 1 -у 2). т.е. Вектор (А,В) называется нормальным вектором прямой l .

Рассмотрим вектор =(-В,А). Тогда

А(-В)+ВА=0. т.е. ^ .

Следовательно, вектор =(-В,А) является направляющим вектором пряной l .

Параметрическое и каноническое уравнения прямой

Уравнение прямой, проходящей через две заданные точки

Пусть в афинной системе координат (0, X, Y) задана прямая l , ее направлящий вектор = (m,n) и точка M 0 (x 0 ,y 0) принадлежащая l . Тогда для произвольной точки M (x ,у ) этой прямой имеем

и так как то .

Если обозначить и

Радиус-векторы соответственно точек M и M 0 , то

- уравнение прямой в векторной форме.

Так как =(х ,у ), =(х 0 ,у 0), то

x = x 0 + mt ,

y = y 0 + nt

- параметрическое уравнение прямой .

Отсюда следует, что

- каноническое уравнение прямой .

Наконец, если на прямой l заданы две точки M 1 (х 1 ,у 1) и

M 2 (x 2 ,у 2), то вектор =(х 2 -х 1 ,y 2 -у 1) является направляющим вектором прямой l . Тогда

- уравнение прямой проходящей через две заданные точки .

Взаимное расположение двух прямых .

Пусть прямые l 1 и l 2 заданы своими общими уравнениями

l 1: А 1 х + В 1 у + С 1 = 0, (1)

l 2: А 2 х + В 2 у + С 2 = 0.

Теорема . Пусть прямые l 1 и l 2 заданы уравнениями (1). Тогда и только тогда:

1) прямые пересекаются, когда не существует такого числа λ, что

A 1 =λA 2 , В 1 =λB 2 ;

2) прямые совпадают, когда найдется такое число λ, что

А 1 =λA 2 , B 1 =λB 2 , С 1 =λС 2 ;

3) прямые различны и параллельны, когда найдется такое числе λ, что

А 1 =λA 2 , В 1 =λВ 2 , С 1 λС 2 .

Пучок прямых

Пучком прямых называется совокупность всех прямых на плоскости, проходящих через некоторую точку, называемую центром пучка.

Для задания уравнения пучка достаточно знать какие-либо две прямые l 1 и l 2 , проходящие через центр пучка.

Пусть в аффинной системе координат прямые l 1 и l 2 заданы уравнениями

l 1: A 1 x + B 1 y + C 1 = 0,

l 2: A 2 x + B 2 y + C 2 = 0.

Уравнение:

A 1 x + B 1 y + С + λ (A 2 х + В 2 y + C) = 0

- уравнение пучка прямых, определяемого уравнениями l 1 и l 2.

В дальнейшем, под системой координат будем понимать прямоугольную систему координат .

Условия параллельности и перпендикулярности двух прямых

Пусть заданы прямые l 1 и l 2 . своими общими уравненими; = (А 1 ,B 1), = (А 2 ,В 2) – нормальные векторы этих прямых; k 1 = tgα 1 , k 2 = tgα 2 – угловые коэффициенты; = (m 1 ,n 1), (m 2 ,n 2) – направляющие векторы. Тогда, прямые l 1 и l 2 параллельны, в том и только том случае, если выполняется одно из следующих условий:

либо , либо k 1 =k 2 , либо .

Пусть теперь прямые l 1 и l 2 перпендикулярны. Тогда, очевидно, , то есть А 1 А 2 + В 1 В 2 = 0.

Если прямые l 1 и l 2 заданы соответственно уравнениями

l 1: у =k 1 x + b 1 ,

l 2: у =k 2 x + b 2 ,

то tgα 2 = tg(90º+α) = .

Отсюда следует, что

Наконец, если и направляющие векторы прямых, то ^ , то есть

m 1 m 2 + n 1 n 2 = 0

Последнее соотношения выражают необходимое и достаточное условие перпендикулярности двух плоскостей.

Угол между двумя прямыми

Под углом φ между двумя прямыми l 1 и l 2 будем понимать наименьший угол, на который надо повернуть одну прямую, чтобы она стала параллельной другой прямой или совпала с ней, то есть 0 £ φ £

Пусть прямые заданы общими уравнениями. Очевидно, что

cosφ=

Пусть теперь прямые l 1 и l 2 задана уравнениями с угловыми коэффициентами k 1 в k 2 соответственно. Тогда

Очевидно, что , то есть (х -х 0) + В(у -у 0) + C(z -z 0) = 0

Раскроем скобки и обозначим D= -Аx 0 - Ву 0 - Cz 0 . Получим

Ax + By + Сz + D = 0 (*)

- уравнение плоскости в общем виде или общее уравнение плоскости .

Теорема 3.1 Линейное уравнение (*) (A 2 +B 2 +C 2 ≠ 0) является уравнением плоскости и обратно, любое уравнение плоскости является линейным.

1) D = 0, тогда плоскость проходит через начало координат.

2) А = 0, тогда плоскость параллельна оси ОХ

3) А = 0, В = 0, тогда плоскость параллельна плоскости OXY.

Пусть в уравнении все коэффициенты отличны от нуля.

- уравнение плоскости в отрезках . Числа |а|, |b|, |с| указывают на величины отрезков, отсекаемых плоскостью на координатных осях.

Если в общем уравнении прямой Ах + Ву + С = 0 С ¹ 0, то, разделив на –С, получим: или

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется нормирующем множителем , то получим

Xcosj + ysinj - p = 0 –

нормальное уравнение прямой.

Знак ± нормирующего множителя надо выбирать так, чтобы m×С < 0.

р – длина перпендикуляра, опущенного из начала координат на прямую, а j - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.

уравнение этой прямой в отрезках:

уравнение этой прямой с угловым коэффициентом: (делим на 5)

нормальное уравнение прямой:

; cosj = 12/13; sinj = -5/13; p = 5.

Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.

Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см 2 .

Уравнение прямой имеет вид: , a = b = 1; ab/2 = 8; a = 4; -4.

a = -4 не подходит по условию задачи.

Итого: или х + у – 4 = 0.

Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.

Уравнение прямой имеет вид: , где х 1 = у 1 = 0; x 2 = -2; y 2 = -3.

Уравнение прямой, проходящей через данную точку

Перпендикулярно данной прямой.

Определение. Прямая, проходящая через точку М 1 (х 1 , у 1) и перпендикулярная к прямой у = kx + b представляется уравнением:

Угол между прямыми на плоскости.

Определение. Если заданы две прямые y = k 1 x + b 1 , y = k 2 x + b 2 , то острый угол между этими прямыми будет определяться как

Две прямые параллельны, если k 1 = k 2 .

Две прямые перпендикулярны, если k 1 = -1/k 2 .

Теорема. Прямые Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 параллельны, когда пропорциональны коэффициенты А 1 = lА, В 1 = lВ. Если еще и С 1 = lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Расстояние от точки до прямой.

Теорема. Если задана точка М(х 0 , у 0), то расстояние до прямой Ах + Ву + С =0 определяется как

Доказательство. Пусть точка М 1 (х 1 , у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М 1:

Координаты x 1 и у 1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x 0) + B(y – y 0) + Ax 0 + By 0 + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.

Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.

k 1 = -3; k 2 = 2 tgj = ; j = p/4.

Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Находим: k 1 = 3/5, k 2 = -5/3, k 1 k 2 = -1, следовательно, прямые перпендикулярны.

Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

Находим уравнение стороны АВ: ; 4x = 6y – 6;

2x – 3y + 3 = 0;

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.

k = . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

Ответ: 3x + 2y – 34 = 0.

Кривые второго порядка.

Кривая второго порядка может быть задана уравнением

Ах 2 + 2Вху + Су 2 + 2Dx + 2Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) - уравнение эллипса.

2) - уравнение “мнимого” эллипса.

3) - уравнение гиперболы.

4) a 2 x 2 – c 2 y 2 = 0 – уравнение двух пересекающихся прямых.

5) y 2 = 2px – уравнение параболы.

6) y 2 – a 2 = 0 – уравнение двух параллельных прямых.

7) y 2 + a 2 = 0 – уравнение двух “мнимых” параллельных прямых.

8) y 2 = 0 – пара совпадающих прямых.

9) (x – a) 2 + (y – b) 2 = R 2 – уравнение окружности.

Окружность.

В окружности (x – a) 2 + (y – b) 2 = R 2 центр имеет координаты (a; b).

Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

2x 2 + 2y 2 – 8x + 5y – 4 = 0.

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты:

x 2 + y 2 – 4x + 2,5y – 2 = 0

x 2 – 4x + 4 –4 + y 2 + 2,5y + 25/16 – 25/16 – 2 = 0

(x – 2) 2 + (y + 5/4) 2 – 25/16 – 6 = 0

(x – 2) 2 + (y + 5/4) 2 = 121/16

Отсюда находим О(2; -5/4); R = 11/4.

Эллипс.

Определение. Эллипсом называется кривая, заданная уравнением .

Определение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

F 1 , F 2 – фокусы. F 1 = (c; 0); F 2 (-c; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

a 2 = b 2 + c 2 .

Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, r 1 + r 2 = 2 (по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, r 1 + r 2 = a – c + a + c. Т.к. по определению сумма r 1 + r 2 – постоянная величина, то, приравнивая, получаем:

a 2 = b 2 + c 2

r 1 + r 2 = 2a.

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .

Т.к. с < a, то е < 1.

Определение. Величина k = b/a называется коэффициентом сжатия эллипса, а величина 1 – k = (a – b)/a называется сжатием эллипса.

Коэффициент сжатия и эксцентриситет связаны соотношением: k 2 = 1 – e 2 .

Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

Если для точки М(х 1 , у 1) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне эллипса.

Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения :

R 1 = a – ex, r 2 = a + ex.

Доказательство. Выше было показано, что r 1 + r 2 = 2a. Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

Аналогично доказывается, что r 2 = a + ex. Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами . Их уравнения:

X = a/e; x = -a/e.

Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением:

1) Координаты нижней вершины: x = 0; y 2 = 16; y = -4.

2) Координаты левого фокуса: c 2 = a 2 – b 2 = 25 – 16 = 9; c = 3; F 2 (-3; 0).

3) Уравнение прямой, проходящей через две точки:

Пример. Составить уравнение эллипса, если его фокусы F 1 (0; 0), F 2 (1; 1), большая ось равна 2.

Уравнение эллипса имеет вид: . Расстояние между фокусами:

2c = , таким образом, a 2 – b 2 = c 2 = ½

по условию 2а = 2, следовательно а = 1, b =

Гипербола.

Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

По определению ïr 1 – r 2 ï= 2a. F 1 , F 2 – фокусы гиперболы. F 1 F 2 = 2c.

Выберем на гиперболе произвольную точку М(х, у). Тогда:

обозначим с 2 – а 2 = b 2 (геометрически эта величина – меньшая полуось)

Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых

Определение. Отношение называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с 2 – а 2 = b 2:

Если а = b, e = , то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.

Из очевидных геометрических соотношений можно записать:

a/e + d = x, следовательно d = x – a/e.

(x – c) 2 + y 2 = r 2

Из канонического уравнения: , с учетом b 2 = c 2 – a 2:

Тогда т.к. с/a = e, то r = ex – a.

Для левой ветви гиперболы доказательство аналогично. Теорема доказана.

Пример. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса .

Для эллипса: c 2 = a 2 – b 2 .

Для гиперболы: c 2 = a 2 + b 2 .

Уравнение гиперболы: .

Пример. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением параметром параболы. Выведем каноническое уравнение параболы.

Из геометрических соотношений: AM = MF; AM = x + p/2;

MF 2 = y 2 + (x – p/2) 2

(x + p/2) 2 = y 2 + (x – p/2) 2

x 2 +xp + p 2 /4 = y 2 + x 2 – xp + p 2 /4

Уравнение директрисы: x = -p/2.

Пример. На параболе у 2 = 8х найти точку, расстояние которой от директрисы равно 4.

Из уравнения параболы получаем, что р = 4.

r = x + p/2 = 4; следовательно:

x = 2; y 2 = 16; y = ±4. Искомые точки: M 1 (2; 4), M 2 (2; -4).

Пример. Уравнение кривой в полярной системе координат имеет вид:

Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.

Воспользуемся связью декартовой прямоугольной и полярной системы координат: ;

Получили каноническое уравнение гиперболы. Из уравнения видно, что гипербола сдвинута вдоль оси Ох на 5 влево, большая полуось а равна 4, меньшая полуось b равна 3, откуда получаем c 2 = a 2 + b 2 ; c = 5; e = c/a = 5/4.

Фокусы F 1 (-10; 0), F 2 (0; 0).

Построим график этой гиперболы.

И подробно разберем особый вид уравнения прямой – . Начнем с вида уравнения прямой в отрезках и приведем пример. После этого остановимся на построении прямой линии, которая задана уравнением прямой в отрезках. В заключении покажем, как осуществляется переход от полного общего уравнения прямой к уравнению прямой в отрезках.

Навигация по странице.

Уравнение прямой в отрезках – описание и пример.

Пусть на плоскости зафиксирована Oxy .

Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид , где a и b - некоторые отличные от нуля действительные числа.

Уравнение прямой в отрезках не случайно получило такое название - абсолютные величины чисел a и b равны длинам отрезков, которые отсекает прямая на координатных осях Ox и Oy , считая от начала координат.

Поясним этот момент. Мы знаем, что координаты любой точки прямой удовлетворяют уравнению этой прямой. Тогда отчетливо видно, что прямая, заданная уравнением прямой в отрезках, проходит через точки и , так как и . А точки и как раз расположены на координатных осях Ox и Oy соответственно и удаленны от начала координат на a и b единиц. Знаки чисел a и b указывают направление, в котором следует откладывать отрезки. Знак «+» означает, что отрезок откладывается в положительном направлении координатной оси, знак «-» означает обратное.

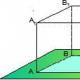
Изобразим схематический чертеж, поясняющий все вышесказанное. На нем показано расположение прямых относительно фиксированной прямоугольной системы координат Oxy в зависимости от значений чисел a и b в уравнении прямой в отрезках.

Теперь стало понятно, что уравнение прямой в отрезках позволяет легко производить построение этой прямой линии в прямоугольной системе координат Oxy . Чтобы построить прямую линию, которая задана уравнением прямой в отрезках вида , следует отметить в прямоугольной системе координат на плоскости точки и , после чего соединить их прямой линией с помощью линейки.

Приведем пример.

Пример.

Постройте прямую линию, заданную уравнением прямой в отрезках вида .

Решение.

По заданному уравнению прямой в отрезках видно, что прямая проходит через точки . Отмечаем их и соединяем прямой линией.

Приведение общего уравнения прямой к уравнению прямой в отрезках.

При решении некоторых задач, связанных с прямой на плоскости, удобно работать с уравнением прямой в отрезках. Однако существуют другие виды уравнений, задающих прямую на плоскости. Поэтому приходится осуществлять переход от заданного уравнения прямой к уравнению этой прямой в отрезках.

В этом пункте мы покажем, как получить уравнение прямой в отрезках, если дано полное общее уравнение прямой .

Пусть нам известно полное общее уравнение прямой на плоскости . Так как А , В и С не равны нулю, то можно перенести число С в правую часть равенства, разделить обе части полученного равенства на –С , а коэффициенты при x и y отправить в знаменатели:
.

(В последнем переходе мы пользовались равенством ).

Так мы от общего уравнения прямой перешли к уравнению прямой в отрезках , где .

Пример.

Прямая в прямоугольной системе координат Oxy задана уравнением . Напишите уравнение этой прямой в отрезках.

Решение.

Перенесем одну вторую в правую часть заданного равенства: . Теперь разделим на обе части полученного равенства: . Осталось преобразовать полученное равенство к нужному виду: . Так мы получили требуемое уравнение прямой в отрезках.

Ответ:

Если прямую определяет