Общий вид уравнения гиперболы. Что такое гипербола, примеры из литературы и повседневной жизни. Примеры гипербол в рекламе

1. Гипербола лежит за полосой со сторонами x = ± a .

Действительно, согласно уравнению гиперболы, имеет место неравенство

2. Гипербола является симметричной относительно начала координат и относительно координатных осей. Это вытекает из того, что в уравнение гиперболы переменные x и y входят в квадратах х 2 и у 2 , и уравнению гиперболы удовлетворяют точки с координатами (х , у ),

(− х , у ), (х , − у ), (− х , − у ).

3. Гипербола имеет две асимптоты

к которым приближаются точки гиперболы при удалении их от начала координат.

4. Оси симметрии называются осями гиперболы, а центр симметрии (точка пересечения осей) - центром гиперболы. Одна из осей пересекается с гиперболой в двух точках А и С, которые называются ее вершинами. Эта ось называется действительной осью гиперболы. Другая ось не имеет общих точек с гиперболой и называется мнимой осью гиперболы. Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы. Величины а и b называются, соответственно, действительной и мнимой полуосями.

5. Гипербола с равными полуосями а = b называется равносторонней и ее каноническое уравнение имеет вид

x 2 − y 2 = a 2 .

Так как основной прямоугольник равносторонней гиперболы является квадратом, то асимптоты равносторонней гиперболы перпендикулярны друг другу.

Эксцентриситет гиперболы (как и эллипса) обозначим буквой ε. Так как с > а : то ε > 1, т. е. эксцентриситет гиперболы больше единицы. Очевидно,

Из последнего равенства легко получается геометрическое истолкование эксцентриситета гиперболы. Чем меньше эксцентриситет, т. е. чем ближе он к единице, тем меньше отношение b ⁄ a , а это означает, что основной прямоугольник более вытянут в направлении действительной оси. Таким образом, эксцентриситет гиперболы характеризует форму ее основного прямоугольника, а, значит, и форму самой гиперболы.

В случае равносторонней гиперболы (a = b ) ε = √2.

ОПР 2. . Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии а ⁄ ε от него, называются директрисами гиперболы.

Установленное свойство эллипса и гиперболы можно положить в основу общего определения этих линий: множество точек, для которых отношение расстояний до фокуса и до соответствующей директрисы является величиной постоянной, равной ε, является эллипсом, если ε < 1, и гиперболой, если ε > 1.

Гипербола представляет собой плоскую кривую, для каждой точки которой модуль разности расстояний до двух заданных точек (фокусов гиперболы ) является постоянным. Расстояние между фокусами гиперболы называется фокусным расстоянием и обозначается через \(2c\). Середина отрезка, соединяющего фокусы, называется центром . У гиперболы имеются две оси симметрии: фокальная или действительная ось, проходящая через фокусы, и перпендикулярная ей мнимая ось, проходящая через центр. Действительная ось пересекает ветви гиперболы в точках, которые называются вершинами . Отрезок, соединяющий центр гиперболы с вершиной, называется действительной полуосью и обозначается через \(a\). Мнимая полуось обозначается символом \(b\). Каноническое уравнение гиперболы записывается в виде
\(\large\frac{{{x^2}}}{{{a^2}}}\normalsize - \large\frac{{{y^2}}}{{{b^2}}}\normalsize = 1\).

Модуль разности расстояний от любой точки гиперболы до ее фокусов является постоянной величиной:
\(\left| {{r_1} - {r_2}} \right| = 2a\),
где \({r_1}\), \({r_2}\) − расстояния от произвольной точки \(P\left({x,y} \right)\) гиперболы до фокусов \({F_1}\) и \({F_2}\), \(a\) − действительная полуось гиперболы.



Уравнения асимптот гиперболы
\(y = \pm \large\frac{b}{a}\normalsize x\)

Соотношение между полуосями гиперболы и фокусным расстоянием
\({c^2} = {a^2} + {b^2}\),
где \(c\) − половина фокусного расстояния, \(a\) − действительная полуось гиперболы, \(b\) − мнимая полуось.

Эксцентриситет гиперболы
\(e = \large\frac{c}{a}\normalsize > 1\)

Уравнения директрис гиперболы
Директрисой гиперболы называется прямая, перпендикулярная ее действительной оси и пересекающая ее на расстоянии \(\large\frac{a}{e}\normalsize\) от центра. У гиперболы − две директрисы, отстоящие по разные стороны от центра. Уравнения директрис имеют вид
\(x = \pm \large\frac{a}{e}\normalsize = \pm \large\frac{{{a^2}}}{c}\normalsize\).

Уравнение правой ветви гиперболы в параметрической форме
\(\left\{ \begin{aligned} x &= a \cosh t \\ y &= b \sinh t \end{aligned} \right., \;\;0 \le t \le 2\pi\),
где \(a\), \(b\) − полуоси гиперболы, \(t\) − параметр.

Общее уравнение гиперболы
где \(B^2 - 4AC > 0\).


Общее уравнение гиперболы, полуоси которой параллельны осям координат
\(A{x^2} + C{y^2} + Dx + Ey + F = 0\),
где \(AC

Равнобочная гипербола
Гипербола называется равнобочной , если ее полуоси одинаковы: \(a = b\). У такой гиперболы асимптоты взаимно перпендикулярны. Если асимптотами являются горизонтальная и вертикальная координатные оси (соответственно, \(y = 0\) и \(x = 0\)), то уравнение равнобочной гиперболы имеет вид
\(xy = \large\frac{{{e^2}}}{4}\normalsize\) или \(y = \large\frac{k}{x}\normalsize\), где \(k = \large\frac{e^2}{4}\normalsize .\)



Параболой называется плоская кривая, в каждой точки которой выполняется следующее свойство: расстояние до заданной точки (фокуса параболы ) равно расстоянию до заданной прямой (директрисы параболы ). Расстояние от фокуса до директрисы называется параметром параболы и обозначается через \(p\). Парабола имеет единственную ось симметрии, которая пересекает параболу в ее вершине . Каноническое уравнение параболы имеет вид
\(y = 2px\).

Уравнение директрисы
\(x = - \large\frac{p}{2}\normalsize\),


Координаты фокуса
\(F \left({\large\frac{p}{2}\normalsize, 0} \right)\)

Координаты вершины
\(M \left({0,0} \right)\)



Общее уравнение параболы
\(A{x^2} + Bxy + C{y^2} + Dx + Ey + F = 0\),
где \(B^2 - 4AC = 0\).


Уравнение параболы, ось симметрии которой параллельна оси \(Oy\)
\(A{x^2} + Dx + Ey + F = 0\;\left({A \ne 0, E \ne 0} \right) \),
или в эквивалентной форме
\(y = a{x^2} + bx + c,\;\;p = \large\frac{1}{2a}\normalsize\)

Уравнение директрисы
\(y = {y_0} - \large\frac{p}{2}\normalsize\),
где \(p\) − параметр параболы.

Координаты фокуса
\(F\left({{x_0},{y_0} + \large\frac{p}{2}\normalsize} \right)\)

Координаты вершины
\({x_0} = - \large\frac{b}{{2a}}\normalsize,\;\;{y_0} = ax_0^2 + b{x_0} + c = \large\frac{{4ac - {b^2}}}{{4a}}\normalsize\)



Уравнение параболы с вершиной в начале координат и осью симметрии, параллельной оси \(Oy\)
\(y = a{x^2},\;\;p = \large\frac{1}{{2a}}\normalsize\)

Уравнение директрисы
\(y = - \large\frac{p}{2}\normalsize\),
где \(p\) − параметр параболы.

Координаты фокуса
\(F \left({0, \large\frac{p}{2}\normalsize} \right)\)

Координаты вершины
\(M \left({0,0} \right)\)

Здравствуйте, уважаемые читатели блога сайт. Все мы в жизни хоть раз говорили или слышали подобные выражение (а кто-то и не раз): ВЕЧНО ОПАЗДЫВАЕТЕ или СТО ЛЕТ НЕ ВИДЕЛИСЬ.

И мало кто задумывался, что эти фразы лишены какого-то здравого смысла. Так, человек просто не может «вечно опаздывать». И не может кто-то не видиться «сто лет», хотя бы потому, что люди редко так долго живут.

Подобные преувеличения в русском языке называются гиперболами и именно о них пойдет речь в этой публикации.

Гипербола - это красивое преувеличение

Само это слово греческое – «hyperbole» и обозначает оно «чрезмерность, избыток, преувеличение».

Гипербола – это одно из средств усиления эмоциональной оценки , заключающееся в чрезмерном преувеличении каких-либо явлений, качеств, свойств или процессов. Благодаря этому создается более впечатляющий образ.

Причем часто преувеличение доходит до совершенно непостижимых понятий, иногда даже . Любой иностранец, если будет переводить дословно, будет явно озадачен. Мы же давно к ним привыкли, и воспринимаем их как совершенно нормальные.

Вот примеры наиболее часто используемых в обиходе гипербол:

НАПУГАТЬ ДО СМЕРТИ
ТЫСЯЧА ИЗВИНЕНИЙ
ХОТЬ ЗАЛЕЙСЯ
РЕКИ КРОВИ
ГОРЫ ТРУПОВ
ЖДУ ЦЕЛУЮ ВЕЧНОСТЬ
ЕХАТЬ ЗА ТЫСЯЧУ КИЛОМЕТРОВ
ВЕСЬ ДЕНЬ ПРОСТОЯЛА
КУЧА ДЕНЕГ
ПИР НА ВЕСЬ МИР
МОРЕ СЛЕЗ
НЕ ВИДЕЛИСЬ 100 ЛЕТ
ОКЕАН СТРАСТЕЙ
ВЕСИТ СТО ПУДОВ
ЗАДУШИТЬ В ОБЪЯТЬЯХ
ИСПУГАТЬСЯ ДО СМЕРТИ

Все перечисленные выражения мы постоянно используем в разговорной речи. И ради эксперимента просто попробуйте разобрать их дословно и увидите, насколько некоторые из них смешны, а порой и абсурдны.

Ну, например, «хоть залейся» — это должно быть такое количество жидкости, чтобы ее хватило на целый бассейн, в который можно было бы погрузиться с головой. Хотя на самом деле мы этим выражением просто хотим сказать, что напитков у нас много — даже больше чем нужно.

Или фраза «куча денег» на самом ведь деле обозначает просто хорошее финансовое состояние, а не то, что человек собрал все свои сбережения и давай их складывать в одну кучу.

А выражение «ехать за тысячу километров» мы употребляем, ни когда речь идет о реальном расстоянии, например, от Москвы до Волгограда или Ростова-на-Дону. А просто в значении «далеко», хотя на самом деле в реальных цифрах там расстояние может быть всего в несколько километров.

И так можно «развенчать» абсолютно любую гиперболу. Но делать этого не стоит. Они и не должны означать абсолютную правду, их задача – наиболее живописно охарактеризовать конкретную ситуацию или мысль, усиливая ее эмоциональный окрас .

Примеры гипербол в художественной литературе

На самом деле подобные преувеличения – это очень старый литературный прием. Он использовался , а это было без малого тысячу лет назад. С помощью гипербол многократно усиливали силу богатырей и их противников.

Сон богатырский длился 12 ДНЕЙ (ну не может человек спать почти две недели)

На пути богатыря стояли силы несметные – ВОЛК ИХ ЗА ДЕНЬ НЕ ОБЕЖИТ, ВОРОН ЗА ДЕНЬ НЕ ОБЛЕТИТ (это сколько врагов должно быть – миллион?)

Махнет богатырь рукой – СРЕДИ ВРАГОВ УЛИЦА, махнет другой – ПЕРЕУЛОК (то есть одним ударом богатырь убивает сразу несколько десятков)

Взял Илья Муромец палицу ВЕСОМ СТО ПУДОВ (тут надо понимать, что сто пудов – это полторы тонны)

Соловей-разбойник свистит – ЛЕС К ЗЕМЛЕ КЛОНИТСЯ, а ЛЮДИ МЕРТВЫМИ ПАДАЮТ (ну тут совсем что-то из разряда сказки)

Точно такие же гиперболы встречаются и в «Слове о полку Игореве» . Например:

«Русичи червлеными щитами перегородили широкие поля, ища себе честь, а князю славы» или «Войско такое, что можно Волгу веслами расплескать, а Дон вычерпать шлемами».

Среди писателей больше всего гипербол встречается у Николая Васильевича Гоголя . Преувеличения есть практически в каждом его известном произведении. Вот, например, он описывает реку Днепр:

Редкая птица долетит до середины Днепра.
Днепр как дорога без конца в длину и без меры в ширину.

Или использует преувеличения в своих , вкладывая их в уста героев:

В муку бы вас все стер! (Городничий)
Тридцать пять тысяч одних курьеров… Меня сам государственный совет боится. (Хлестаков)

А в «Мертвых душах» есть такие слова: «Бесчисленны человеческие страсти как морские пески».

Гиперболы использует практически любой писатель или поэт. С их помощью они, например, более красочно описывают характер героев произведений или показывают свое авторское отношение к ним.

Причем писатели зачастую не используют уже устоявшиеся выражения, а стараются придумать что-то свое.

Вот еще примеры гипербол в литературе :

1. И ядрам пролетать мешала гора кровавых тел (Лермонтов)
2. Закат пылал во сто сорок солнц (Маяковский)
3. Миллион терзаний (Грибоедов)
4. Порядочный человек за вас за тридевять земель готов убежать (Достоевский)
5. И сосна до звезд достает (Мандельштам)
6. Во сне дворник стал тяжелым как комод (Ильф и Петров)

Примеры гипербол в рекламе

Конечно, мимо такого интересного приема, который позволяет усилить реальное значение слов , не могли пройти и рекламщики. Масса слоганов основана на этом принципе. Ведь задача – привлечь внимание клиента, обещая при этом «золотые горы» и всячески подчеркивая уникальность товара:

1. Вкус на грани возможного (жевательная резинка «Стиморол»)
2. Контроль над стихией (кроссовки «Адидас»)
3. Король салатов (майонез «Оливьез»)

В создании рекламных роликов также часто используется принцип гиперболы. Например, серия знаменитых видео про батончики «Сникерс» со слоганом «Ты не ты, когда голоден». Там, где различные персонажи превращаются в совершенно других людей и начинают творить всякие глупости, и только шоколадный батончик способен вернуть их в привычную русло.

В этих роликах явно гиперболизировано (сильно преувеличено) чувство голода и «чудодейственная» сила самого «Сникерса».

Ну и самый простой пример гипербол, который применяют в рекламе, это выражения типа «самый лучший», «самый стильный», «самый комфортный» и так далее, а про цены, наоборот, говорят «самые низкие».

Вместо заключения

Придать большую выразительность и эмоциональную окраску любому выражению можно не только с помощью гиперболы. Есть в русском языке прием, который является ее полной противоположностью. Он не преувеличивает, а, наоборот, уменьшает значение.

Не успеешь глазом моргнуть, а годы уже пролетели.

Называется такой прием « ». Об этом подробно – в нашей следующей статье.

Удачи вам! До скорых встреч на страницах блога сайт

Вам может быть интересно

Что такое инсинуация: значение слова, характеристика, примеры Многозначные слова - это примеры разных граней русского языка Синекдоха - это пример метонимии в русском языке Фамильярность: значение слова, примеры Профанация - это невежество профанов, которые считают способным оскорблять то, что не доступно их пониманию Что такое риторический вопрос и для чего он предназначен Эвфемизм - это фиговый листок русского языка Аллюзии - это новое с намеком на старое Ассонанс - это единство гласных Диалектизмы - это слова с местным колоритом Литота - это преуменьшение и смягчение для создания образа

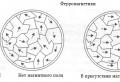
Гиперболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению

Параметры гиперболы:

Точки F 1 (–c, 0), F 2 (c , 0), где называются фокусами гиперболы, при этом величина 2с (с > a > 0) определяет междуфокусное расстояние . Точки А 1 (–а , 0), А 2 (а , 0) называются вершинами гиперболы , при этом А 1 А 2 = 2а образует действительную ось гиперболы, а В 1 В 2 = 2b – мнимую ось (В 1 (0, –b ), B 2 (0, b )), О – центр гиперболы.

Величина называется эксцентриситетом гиперболы, она характеризует меру «сжатости» гиперболы;

– фокальные радиусы гиперболы (точка М принадлежит гиперболе), причем r 1 = a + εx , r 2 = –a + εx для точек правой ветви гиперболы, r 1 = – (a + εx ), r 2 = – (–a + εx ) – для точек левой ветви;

– директрисы гиперболы;

– уравнения асимптот .

Для гиперболы справедливо: ε > 1, директрисы не пересекают границу и внутреннюю область гиперболы, а также обладают свойством

Говорят, что уравнение

задает уравнение гиперболы, сопряженной данной (рис. 20). Его можно записать также в виде

В таком случае ось мнимая, фокусы лежат на оси . Все остальные параметры определяются аналогично как для гиперболы (25).

Точки гиперболы обладают важным характеристическим свойством: абсолютное значение разности расстояний от каждой из них до фокусов есть величина постоянная, равная 2a (рис. 19).

Для параметрического задания гиперболы в качестве параметра t может быть взята величина угла между радиус-вектором точки, лежащей на гиперболе, и положительным направлением оси Ox :

Пример 1. Привести уравнение гиперболы

9x 2 – 16y 2 = 144

к каноническому виду, найти еепараметры, изобразить гиперболу.

Решение. Разделим левую и правую части заданного уравнения на 144: Из последнего уравнения непосредственно следует: a = 4, b = 3, c = 5, O (0, 0) – центр гиперболы. Фокусы находятся в точках F 1 (–5, 0) и F 2 (5, 0), эксцентриситет ε = 5/4, директрисы D 1 и D 2 описываются уравнениями D 1: x = –16/5, D 2: x = 16/5, асимптоты l 1 и l 2 имеют уравнения

Сделаем чертеж. Для этого по осям Ox и Oy симметрично относительно точки (0, 0) отложим отрезки А 1 А 2 = 2а = 8 и В 1 В 2 = 2b = 6 соответственно. Через полученные точки А 1 (–4, 0), А 2 (4, 0), В 1 (0, –3), В 2 (0, 3) проведем прямые, параллельные координатным осям. В результате получим прямоугольник (рис. 21), диагонали которого лежат на асимптотах гиперболы. Строим гиперболу

Для нахождения угла φ между асимптотами гиперболы воспользуемся формулой

.

,

откуда получаем

Пример 2. Определить тип, параметры и расположение на плоскости кривой, уравнение которой

Решение. С помощью метода выделения полных квадратов упростим правую часть данного уравнения:

Получаем уравнение

которое делением на 30 приводится к виду

Это уравнение гиперболы, центр которой лежит в точке действительная полуось – мнимая полуось – (рис. 22).

Пример 3. Составить уравнение гиперболы, сопряженной относительно гиперболы определить ее параметры и сделать чертеж.

Решение. Уравнение гиперболы, сопряженной данной, –

Действительная полуось b = 3, мнимая – а = 4, половина междуфокусного расстояния Вершинами гиперболы служат точки B 1 (0, –3) и В 2 (0, 3); ее фокусы находятся в точках F 1 (0, –5) и F 2 (0, 5); эксцентриситет ε = с /b = 5/3; директрисы D 1 и D 2 задаются уравнениями D 1: y = –9/5, D 2: y = 9/5; уравнения являются уравнениями асимптот (рис. 23).

Заметим, что для сопряженных гипербол общими элементами являются вспомогательный «прямоугольник» и асимптоты.

Пример 4. Написать уравнение гиперболы с полуосями a и b (a > 0, b > 0), если известно, что ее главные оси параллельны координатным осям. Определить основные параметры гиперболы.

Решение. Искомое уравнение можно рассматривать как уравнение гиперболы которое получается в результате параллельного переноса старой системы координат на вектор где (x 0 , y 0) – центр гиперболы в «старой» системе координат. Тогда, используя соотношения между координатами произвольной точки М плоскости в заданной и преобразованной системах

Гипербола и ее свойства

Конспект лекции 14.

Гипербола и парабола и их свойства. Уравнения эллипса, гиперболы и параболы в полярной системе координат.

Литература. § 20, 21.

Определœение 1. Гиперболой принято называть множество точек плоскости, для каждой из которых модуль разности расстояний до двух фиксированных точек и, принадлежащих той же плоскости, является постоянной величиной, меньшей расстояния между точками и.

Точки и,как и в случае эллипса, будем называть фокусами . Очевидно, следует предполагать, что фокусы не совпадают друг с другом. Пусть, а модуль разности расстояний от точки гиперболы до фокусов равен. Тогда, как следует из определœения

Из неравенств, связывающих стороны треугольника, следует, что не существует таких точек М, для которых. Заметим, что эта разность равна в том и только в том случае, когда М лежит на прямой, и не принадлежит отрезку между фокусами. Будем также предполагать, что a ¹ 0, иначе, точки, удовлетворяющие этому условию, образуют серединный перпендикуляр отрезка.

Выведем уравнение гиперболы. Как и в случае эллипса введем прямоугольную декартовую систему координат, которую также будем называть канонической , ось абсцисс которой содержит фокусы и, а ось ординат совпадает с серединным перпендикуляром отрезка (рис. 67). В этой системе координаты фокусов равны: . Точка в том и только в том случае лежат на гиперболе, когда ее координаты удовлетворяют уравнению:

Упростим это уравнение. Раскроем модуль: , и ʼʼуединимʼʼ один из радикалов: . Возведем обе части полученного уравнения в квадрат:

После упрощений получим: . Еще раз возведем обе части в квадрат: , или

В силу неравенства (17.1) , в связи с этим существует число b , для которого

Тогда. Разделив обе части этого равенства на, окончательно получим:

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, координаты любой точки гиперболы удовлетворяют уравнению (17.4). Покажем обратное. Возьмем произвольную точку, координаты которой являются решением этого уравнения. Пусть. Эти числа будем называть фокальными радиусами точки М. Нам следует показать, что. Из уравнения (17.4) следует, что

Так как, то, заменив в данном выражении у по формуле (17.6), получим:

Из формулы (17.3) следует, что. По этой причине. Таким образом,

Аналогично показывается, что

Раскроем модули в полученных формулах. Пусть. Тогда, в связи с этим. Из неравенства (17.5) следует, что. Так как, то перемножая эти неравенства, получим: . Отсюда следует, что. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, и.

Пусть. Тогда и. Из неравенства (17.5) следует, что, перемножая его с неравенством, получим: или. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, и. И в первом и во втором случаях модуль разности фокальных радиусов постоянен и равен. Уравнение (17.4) является уравнением гиперболы. Оно носит название канонического .

Рассмотрим свойства гиперболы, которые позволят построить ее изображение. Вначале найдем ее точки пересечения с осями канонической системы координат. Пусть точка служит точкой пересечения гиперболы с осью абсцисс. Тогда из уравнения (17.4) следует, что, ᴛ.ᴇ. либо, либо. Гипербола пересекается с осью абсцисс в двух точках: . Она не пересекает оси ординат. Действительно, в случае если точка лежит на гиперболе, то число удовлетворяет уравнению: , ĸᴏᴛᴏᴩᴏᴇ не имеет действительных корней. Точки и называются вершинами гиперболы, а числа а и b ‑ ее действительной и мнимой полуосями .

В случае если точка лежит на гиперболе, то, как следует из ее канонического уравнения, точки и также лежат на гиперболе. Отсюда следует, что гипербола симметрична, относительно осœей и центрально симметрична относительно начала канонической системы координат. По этой причине достаточно построить точки гиперболы, лежащие в первой координатной четверти, а затем отразить их симметрично относительно осœей и начала системы координат. Из формулы (17.6) следует, что в этой четверти гипербола совпадает с графиком функции. Средствами математического анализа доказывается, что при эта функция является непрерывной, гладкой и возрастающей. Вместе с тем, она имеет асимптоту. Как доказывается в курсе математического анализа, прямая тогда и только тогда служит асимптотой функции при, когда В данном случае

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, прямая ‑асимптота гиперболы в первой координатной четверти. Так как гипербола симметрична относительно координатных осœей, то эта же прямая служит ее асимптотой в третьей четверти, а прямая ‑ ее асимптота во второй и четвертой четвертях. Гипербола изображена на рисунке 67.

Укажем способ построения точек гиперболы циркулем и линœейкой. Пусть и ‑ ее фокусы, и - точки пересечения с осью абсцисс. Построим окружность a с центром в точке радиуса r . Далее увеличим раствор циркуля на длину отрезка и построим окружность b с центром в точке с радиусом. Ясно, что точки пересечения окружностей a и b лежат на гиперболе. Меняя радиус r можно построить любое число точек гиперболы (рис. 68).

Гипербола, аналогично тому, как и эллипс, обладает директориальным свойством.

Определœение 2. Под эксцентриситетом гиперболы принято понимать число, равное:

Из неравенства (17.1) следует, что для гиперболы (сравните, для эллипса эксцентриситет меньше единицы). Выясним, как меняется форма гиперболы, в случае если ее эксцентриситет принимает значения от 1 до + .. Тогда из формулы (17.9) получим: . Пусть e ® 1, тогда a ® c . Как мы уже отмечали, в данном случае гипербола "сжимается", ее ветви приближаются к двум лучам оси абсцисс, начала которых лежат в ее фокусах. При a ® 0 ветви гиперболы "распрямляются" к серединному перпендикуляру отрезка, ᴛ.ᴇ. к оси ординат.

Определœение 3. Прямые, определœенные уравнениями:

называются директрисами гиперболы.

Считается, что директриса соответствует фокусу, а - фокусу. Так как, то. По этой причине директрисы пересекают ось абсцисс во внутренних точках отрезка, заключенного между вершинами гиперболы (рис. 69). Докажем директориальное свойство гиперболы.

Теорема. Гипербола представляет собой множество всœех точек плоскости, для каждой из которых отношение расстояния от этой точки до фокуса к расстоянию до директрисы, соответствующей этому фокусу, является постоянным числом, равным эксцентриситету.

Доказательство. Пусть дана гипербола. Будем предполагать, что на плоскости выбрана ее каноническая система координат. Рассмотрим точку, лежащую на гиперболе. Обозначим через и ее расстояния до директрис и. Из формулы для вычисления расстояния от точки до прямой (см. § 14) следует, что, . Найдем отношения и, где и ‑ фокальные радиусы точки М . Из равенств (17.7) - (17.9), получим: и. По этой причине.

Покажем обратное. Пусть отношение расстояния от некоторой точки М до фокуса гиперболы к расстоянию от нее до соответствующей директрисы равно эксцентриситету. Проверим, что точка лежит на гиперболе. Доказательство проведем для фокуса и директрисы. Для вторых фокусов и директрисы рассуждения проводятся аналогично. Пусть даны координаты точки: . Тогда. Расстояние до директрисы равно: . Так как, то. Отсюда

Так как (см. (17.3)), то, или. Точка М принадлежит гиперболе, теорема доказана.

Директориальные свойства эллипса и гиперболы позволяют иначе подойти к определœению этих кривых. Из доказанных теорем следует, что если на плоскости даны прямая (директриса) и точка (фокус), которая не лежит на этой прямой, то множество всœех точек плоскости, для каждой из которых отношение расстояния до фокуса к расстоянию до директрисы, равно постоянному числу, представляет собой эллипс, в случае если это число меньше единицы, и гиперболу, в случае если оно больше единицы. Ответ на вопрос, какой вид имеет это множество, в случае если отношение равно единице, будет дан в следующем параграфе.

Ответим на вопрос, какой вид имеет множество точек, для каждой из которых отношении расстояния до точки к расстоянию до прямой, не содержащей эту точку, равно единице. Мы покажем, что такое множество точек хорошо известно из школьного курса алгебры, оно совпадает с параболой.

Определœение 1. Множество точек плоскости, для каждой из которых расстояние до фиксированной точки плоскости равно расстоянию до фиксированной прямой, не содержащей эту точку, принято называть параболой.

Точку и прямую, которые упомянуты в определœении, будем называть соответственно фокусом и директрисой параболы. Будем также считать, что эксцентриситет параболы равен единице. Нетрудно узнать, что представляет собой множество точек, удовлетворяющих определœению 1, в случае если фокус лежит на директрисе. В случае если F - фокус, d ‑ директриса, а М - точка множества, то в данном случае отрезок FM перпендикулярен d . По этой причине такое множество совпадает с прямой, проходящей через фокус перпендикулярной директрисе.

Выведем уравнение параболы. Для этого выберем прямоугольную декартовую систему координат так, чтобы ось абсцисс проходила через фокус F и была перпендикулярна даректрисе d параболы, а ее начало О совпадало с серединой отрезка, заключенного между F и точкой Q пересечения оси абсцисс и директрисы. Направление оси абсцисс определяется вектором (рис. 71). Такую систему координат будем называть канонической . Обозначим через p длину отрезка FQ , Число р принято называть фокальным параметром параболы. Тогда в канонической системе координаты фокуса F и уравнение директрисы d имеет вид: ,

Рассмотрим произвольную точку. расстояние р от М до F равно: . Длина перпендикуляра d, опущенного из M на директрису d , согласно формуле для вычисления расстояния от точки до прямой (см § 14), имеет вид: . По этой причине из определœения 1 следует, что точка М в том и только в том случае лежит на параболе, когда

Уравнение (18.1) представляет собой уравнение параболы. Нам крайне важно его упростить. Для этого возведем обе части в квадрат:

Отсюда следует, что

После приведения подобных членов, получим:

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, в случае если точка принадлежит параболе, то ее координаты удовлетворяют уравнению (18.4). Нетрудно убедиться в обратном. В случае если координаты точки М служат решением уравнения (18.4), то они удовлетворяют уравнениям (18.3) и (18.2). Извлекая квадратный корень из обеих частей равенства (18.2), получим, что координаты точки М удовлетворяют (18.1). Точка лежит на параболе.

Уравнение (18.4) носит название канонического уравнения параболы. Отметим ее свойства. Начало О канонической системы координат лежит на параболе, так как ‑ решение уравнения (18.4). Она принято называть ее вершиной. Парабола симметрична относительно оси абсцисс и не симметрична относительно оси ординат канонической системы. Действительно, в случае если координаты точки удовлетворяют уравнению (18.4), то координаты точки также удовлетворяют уравнению (18.4), а координаты точки не являются решением этого уравнения. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, для построения параболы достаточно изобразить график степенной функции, а затем отобразить его симметрично относительно оси абсцисс. Средствами математического анализа доказывается, что она непрерывная, гладкая и бесконечно возрастающая функция. Парабола изображена на рисунке 71.

Рассмотрим способ построения точек параболы. Пусть F - ее фокус, а d - директриса. Проведем ось симметрии параболы, ᴛ.ᴇ. прямую l , содержащую F и перпендикулярную d . Далее построим несколько прямых перпендикулярных оси. На каждой прямой определим две точки пересечения с окружностью, центр которой находится в фокусе F , а радиус равен расстоянию между этой прямой и директрисой (см. рис. 72). Ясно, что эти точки лежат на параболе.

Пусть кривая g представляет собой эллипс, одну ветвь гиперболы, либо параболу. Пусть F - фокус, а d - директриса кривой g, соответствующая этому фокусу. При этом будем предполагать, что в случае гиперболы фокус и директриса выбраны так, что рассматриваемая ветвь кривой лежит в той же полуплоскости относительно d, что и фокус F . Будем также предполагать, что полюс полярной системы координат совпадает с F, a полярная ось l - лежит на оси симметрии и не пересекает директрису d (рис. 74). Восставим в точке F перпендикуляр к l , Р - точка его пересечения с γ. Обозначим через р длину отрезка FР . Число р будем называть фокальным параметром g.

Обозначим через r и j - полярные координаты точки М . Напомним, что в нашем случае, а j - ориентированный угол между полярной осью l и вектором. Обозначим через Q и N проекции точек Р и М на директрису d , а через К ‑ проекцию М на ось симметрии кривой g (см. рис. 74). Тогда, в случае если R - точка пересечения директрисы d и оси симметрии l , то Так как проекция на l имеет вид: , а, то. Воспользуемся директориальным свойством кривой второго порядка. В случае если e - эксцентриситет g, то. По этой причине, а. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, . Помножив это соотношение на e и выделив r, окончательно получим:

Уравнение (18.6) принято называть полярным уравнением кривой второго порядка g.

Пусть e < 1. Тогда g представляет собой эллипс. В этом случае для любого j: . Так как полярный радиус всœегда положителœен, то для любого угла φ существует значение, ρ определяемое формулой (18.6), для которого точка M (r; j) лежит на эллипсе. Любой луч с началом в полюсе полярной системы координат пересекает эллипс (рис. 75). В случае если e = 1, то g представляет собой - параболу. В этом случае для любого j: , причем при j = 0. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, в уравнении (18.6) j принимает всœе значения на полуинтервале (- p; p] , за исключением 0. Любой луч с началом в фокусе F , за исключением полярной оси, пересекает параболу (рис. 76). Рассмотрим случай, когда e > 1. Тогда g представляет собой ветвь гиперболы. Как следует из уравнения (18.6), угол j удовлетворяет неравенству. Отсюда

Решим это неравенство. Пусть. Так как, то. Воспользуемся формулами, выражающими эксцентриситет гиперболы через ее полуоси и расстояние между фокусами (см. § 17), получим: , ᴛ.ᴇ. . Нетрудно видеть, что j является решением неравенства (18.7) в том и только в том случае, когда, . Геометрически это означает, что если угол φ принадлежит отрезку [ ; ], то луч, составляющий угол j с полярной осью и с началом в фокусе F, не пересекает ветвь гиперболы. Отметим, что лучи, образующие с полярной осью углы, равные и, параллельны асимптотам гиперболы (рис. 77). Можно доказать, что если на плоскости введены обобщенные полярные координаты (см. § 9), то уравнение (18.6) в случае задает вторую ветвь гиперболы.

Гипербола и ее свойства - понятие и виды. Классификация и особенности категории "Гипербола и ее свойства" 2017, 2018.